Касательная — ключевой элемент геометрии — познайте суть, свойства и значение в математическом мире

Касательная – это одно из базовых понятий математики, которое является важным инструментом в геометрии и анализе. Она представляет собой линию, прикладываясь к кривой в определенной точке, и имеет некоторые уникальные свойства и особенности, которые делают ее интересной и полезной.

Касательная также имеет несколько важных свойств. Она всегда касается кривой в одной точке и не пересекает ее. Кроме того, касательная является линией, которая находится в одной плоскости с кривой, и имеет угол наклона, равный производной функции в этой точке. Это позволяет находить производные и делать некоторые вычисления, связанные со скоростью изменения функции.

Касательная: анализ основных причин и свойств

Одной из главных причин изучения касательных является понимание скорости и направления движения объектов. Касательная к кривой в заданной точке показывает направление и величину касательной скорости объекта в этой точке. Это особенно важно в физике, где нужно анализировать движение тел и предсказывать их будущее положение.

Еще одной причиной изучения касательных является анализ формы и поведения кривых. Касательная к кривой в любой ее точке может помочь определить форму кривой, направление ее изгиба и точки экстремума. Это особенно полезно в графическом представлении данных, обработке изображений и моделировании объектов.

Свойства касательных также играют важную роль в математическом анализе и оптимизации функций. Касательная к графику функции в заданной точке позволяет найти производную этой функции в данной точке. Это помогает определить экстремумы функции, ее выпуклость или вогнутость, а также провести анализ точек перегиба.

Причины появления касательных

• Изменение наклона графика: Касательная в каждой точке графика функции отображает изменение наклона функции в этой точке. Таким образом, она помогает нам понять, каким образом меняется значение функции от точки к точке.
• Определение функции в точке: Касательная позволяет нам определить значение функции в конкретной точке. По определению, касательная к графику функции в точке является пределом средних приращений функции в этой точке.
• Аппроксимация значения функции: Касательная позволяет нам приближенно определить значение функции вблизи точки. Такая аппроксимация часто используется в прикладных задачах для быстрого и достаточно точного вычисления значений функции.
• Исследование графика функции: Касательная дает возможность изучать свойства функции в различных точках графика. Наклон касательной может использоваться для определения экстремумов функции, точек перегиба и других особенностей графика.

Все эти причины позволяют нам получить дополнительную информацию о функции и ее поведении в определенных точках. Понимание причин появления касательных помогает нам более глубоко изучить математические объекты и применить их в решении различных задач.

Геометрические факторы определяют направление касательной

Первым геометрическим фактором, который влияет на направление касательной, является кривизна кривой в данной точке. Кривизна определяет степень, с которой кривая «изгибается» в данной точке. Чем больше кривизна, тем сильнее изгиб кривой и тем более крутым будет угол между касательной и осью абсцисс (горизонтальной линией).

Вторым фактором, определяющим направление касательной, является направление движения по кривой в данной точке. Если движение по кривой происходит слева направо, то касательная будет направлена вправо. В случае движения по кривой справа налево, касательная будет направлена влево.

Третьим геометрическим фактором, влияющим на направление касательной, является положение точки касания относительно кривой. Если точка касания находится выше кривой, то касательная будет направлена вниз. В случае, если точка касания находится ниже кривой, касательная будет направлена вверх.

Помимо этих основных геометрических факторов, направление касательной может быть изменено изменением масштаба координатной оси. Например, если масштаб по оси абсцисс уменьшается, то касательная будет стремиться стать вертикальной, и наоборот, при увеличении масштаба она будет стремиться стать горизонтальной.

Таким образом, геометрические факторы, такие как кривизна кривой, направление движения по кривой и положение точки касания, определяют направление касательной в данной точке. Понимание этих факторов позволяет более точно анализировать и исследовать кривые, а также использовать касательные в решении задач геометрии и математического анализа.

Физические законы влияют на формирование касательной

Одним из физических законов, влияющих на формирование касательной, является закон инерции. Согласно этому закону, тело сохраняет свое состояние покоя или равномерного прямолинейного движения, пока на него не действует внешняя сила. Именно этот закон помогает понять, почему касательная к кривой может быть только в одной точке, так как в остальных точках касания тело будет продолжать двигаться по кривой.

Еще одним физическим законом, влияющим на формирование касательной, является закон сохранения энергии. Согласно этому закону, энергия в системе остается постоянной, если внешние силы не совершают работу. Данный закон позволяет объяснить, почему касательная к кривой в точке касания не является вертикальной или горизонтальной, так как такие положения противоречили бы закону сохранения энергии.

Кроме того, на формирование касательной влияет закон динамики. Согласно этому закону, на тело действует сила, равная произведению его массы на ускорение. Применительно к касательной, этот закон объясняет, почему касательная направлена в направлении ускорения кривой в определенной точке.

Таким образом, физические законы играют важную роль в формировании касательной к кривой. Они объясняют, почему касательная имеет определенное направление, почему она касается кривой только в одной точке, а также отличается от горизонтальной или вертикальной прямой. Понимание этих законов позволяет лучше изучить свойства и особенности касательных.

Математические исследования раскрывают функциональные аспекты касательных

Исследования позволили выяснить, что касательные имеют особые свойства. Например, их наклон может меняться в зависимости от точки на кривой, с которой они касаются. Также касательные могут быть использованы для вычисления производной функции в данной точке, что позволяет определить ее скорость изменения.

Кроме того, математические исследования позволяют использовать касательные для решения различных задач. Например, они позволяют определить кривизну графика функции в данной точке, что может быть полезно при анализе поведения функций.

Также исследования показывают, что касательные могут быть использованы для определения точек экстремума функции. Например, точка, в которой касательная пересекает ось абсцисс, может быть точкой минимума или максимума функции.

Однако, чтобы полностью понять функциональные аспекты касательных, необходимо иметь хорошие знания в математике и уметь проводить различные вычисления. Это позволит использовать касательные в анализе функций и решении сложных математических задач.

Свойства и особенности касательных

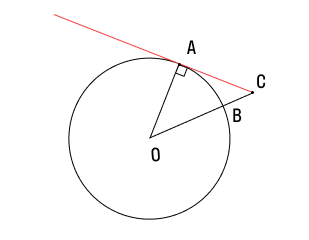
1. Касательная всегда перпендикулярна радиусу кривизны в точке касания. Это означает, что угол, образуемый касательной и радиусом кривизны, равен 90 градусов.
2. Касательная является линией, которая находится в пределах кривой. Она не пересекает кривую, а только касается ее в одной точке.
3. Касательная может быть использована для определения направления и скорости движения объекта на кривой. Например, скорость движения автомобиля на дороге может быть определена с помощью касательной к кривой дороги в данной точке.
4. Касательная может быть использована для нахождения угла наклона кривой в данной точке. Угол наклона касательной является мерой крутизны кривой в этой точке.
5. Касательная может быть построена с использованием производной функции, описывающей кривую. Производная показывает, как меняется функция в зависимости от изменения аргумента.
6. Касательные могут быть построены для разных видов кривых, таких как эллипсы, гиперболы, параболы и т. д. У каждого вида кривой есть свои особенности, которые определяют свойства касательной в этом случае.

Изучение свойств и особенностей касательных позволяет более глубоко понять форму и поведение кривой. Это важно для многих областей науки и техники, таких как физика, инженерия и компьютерная графика.

Точность и прямолинейность — главные характеристики касательной

Прямолинейность касательной означает, что она всегда представляет собой прямую линию. Эта характеристика позволяет нам более удобно работать с функцией, поскольку прямые линии обладают простыми свойствами и уравнениями.

Благодаря точности и прямолинейности касательной, мы можем определить производную функции и использовать ее для решения различных задач. Например, при изучении движения объекта, зная касательную в определенный момент времени, мы можем вычислить скорость и ускорение объекта.

Таким образом, точность и прямолинейность являются важными свойствами касательной, которые позволяют нам более полно и точно анализировать функции и использовать их в различных областях науки и техники.

Вопрос-ответ:

Что такое касательная?

Касательная – это прямая, которая касается кривой в одной точке. Она имеет каждый геометрический смысл и широко применяется в математике и физике.

Как найти уравнение касательной к кривой?

Чтобы найти уравнение касательной к кривой в точке, нужно сначала найти ее координаты. Затем, используя производную функции, найдем угловой коэффициент касательной и составим уравнение вида y = kx + b, подставляя известные значения координат и коэффициент.